commit 1bfc9cf963b822271a6cf7111c6d8cf31a659e56
parent 845b20470e3c57466088262629ee6aee5f86e243
Author: Alex Balgavy <alex@balgavy.eu>
Date: Sat, 2 Apr 2022 15:12:37 +0200
Added notes from a linear algebra article
Diffstat:
2 files changed, 24 insertions(+), 0 deletions(-)
diff --git a/content/lin-algebra-notes/_index.md b/content/lin-algebra-notes/_index.md
@@ -5,6 +5,8 @@ title = 'Linear Algebra'
# Linear Algebra
If you need help with any of the topics, check out [PatrickJMT on Youtube](https://www.youtube.com/user/patrickJMT). He has some of the best math videos on the internet.
+[Preliminary - a great article about why linear algebra is useful and important.](intuitive-guide-to-linear-algebra-notes/)
+
- [Introduction](introduction)
- [Linear Equations](introduction#linear-equations)
- [Matrix notation](introduction#matrix-notation)
diff --git a/content/lin-algebra-notes/intuitive-guide-to-linear-algebra-notes.md b/content/lin-algebra-notes/intuitive-guide-to-linear-algebra-notes.md
@@ -0,0 +1,22 @@
++++
+title = 'Notes from An Intuitive Guide to Linear Algebra'
++++
+# Notes from [An Intuitive Guide to Linear Algebra](https://betterexplained.com/articles/linear-algebra-guide/)
+
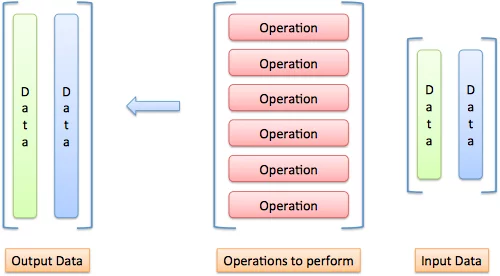
+- Linear algebra gives you mini-spreadsheets for your math equations
+
+ 
+
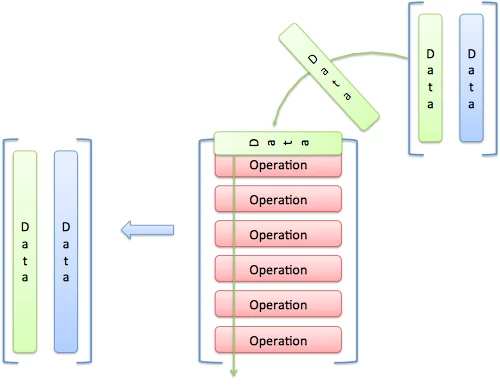
+- Commonly: operations are in rows, data is in columns.
+- Imagine "pouring" each input through each operation:
+
+ 
+
+- A matrix is a single variable representing a spreadsheet of inputs or operations.
+- the beauty of linear algebra is representing an entire spreadsheet calculation with a single letter. Want to apply the same transformation a few times? Use N² or N³.
+- we can treat the operations matrix as inputs! Applying one operations matrix to another gives a new operations matrix that applies both transformations, in order.
+- The determinant is the "size" of the output transformation
+- Transposition is sort of like converting code to data and vice-versa
+- The eigenvector and eigenvalue represent the "axes" of the transformation.
+- An "eigenvector" is an input that doesn't change direction when it's run through the matrix (it points "along the axis"). And although the direction doesn't change, the size might. The eigenvalue is the amount the eigenvector is scaled up or down when going through the matrix.
+